[LG]《Scaling Laws are Redundancy Laws》Y Bi, V D Calhoun [Georgia Institute of Technolog] (2025)
深度学习中的Scaling Laws(缩放律)本质上是冗余定律——这揭示了模型性能提升的数学根源,首次给出清晰闭式表达:
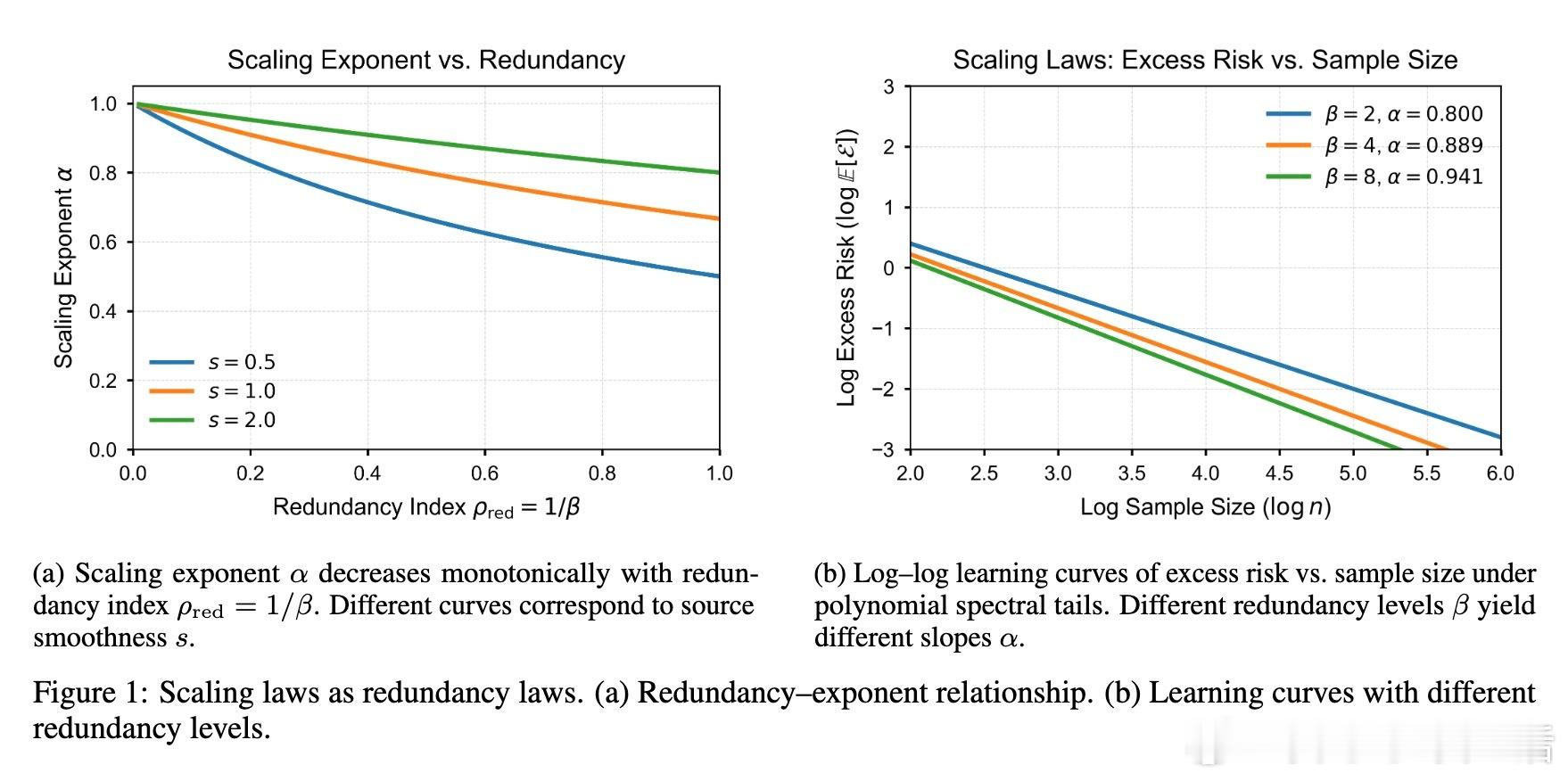
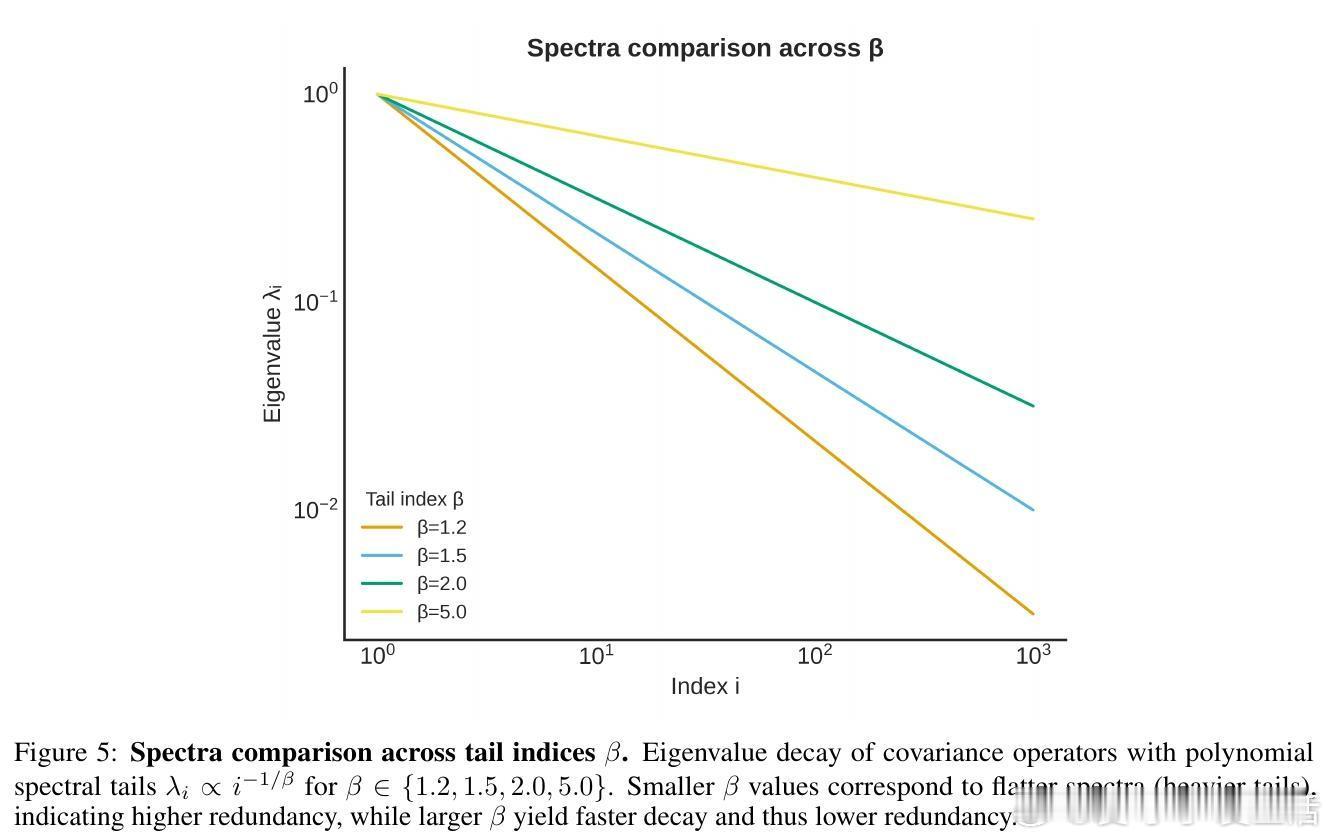
• 学习曲线的幂律指数α=2s / (2s + 1/β),其中s代表目标函数的正则性,β控制数据协方差谱的多项式尾部衰减;1/β即冗余度指标,冗余越大,学习越慢。
• 该指数非普适,而是由数据表示的冗余度主导。谱更陡峭(β更大)意味着更少冗余,更快收益递增。
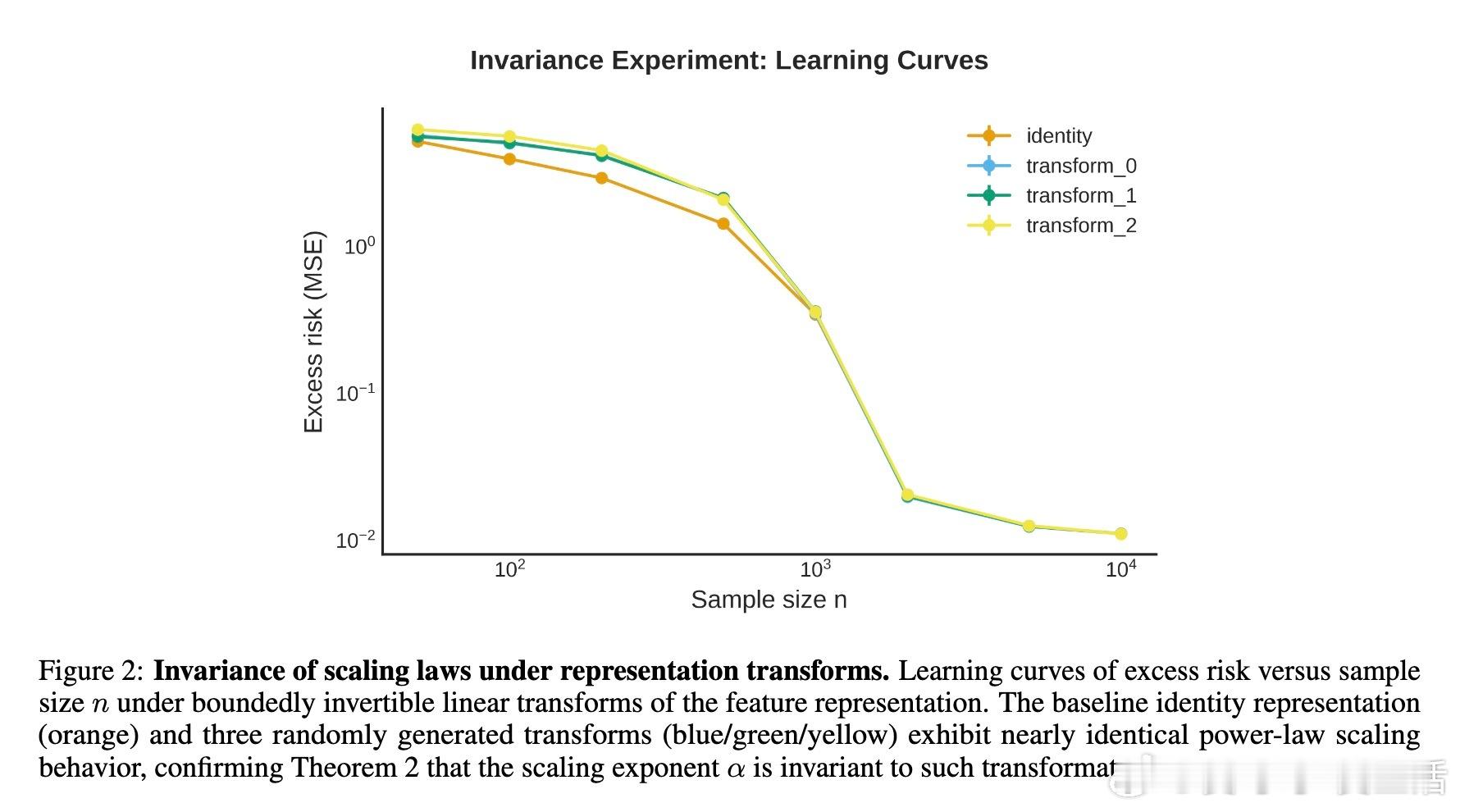
• 定律在有界可逆变换、多模态混合、有限宽度随机特征近似及Transformer的线性化(NTK)和特征学习(核漂移)两种训练阶段均成立。
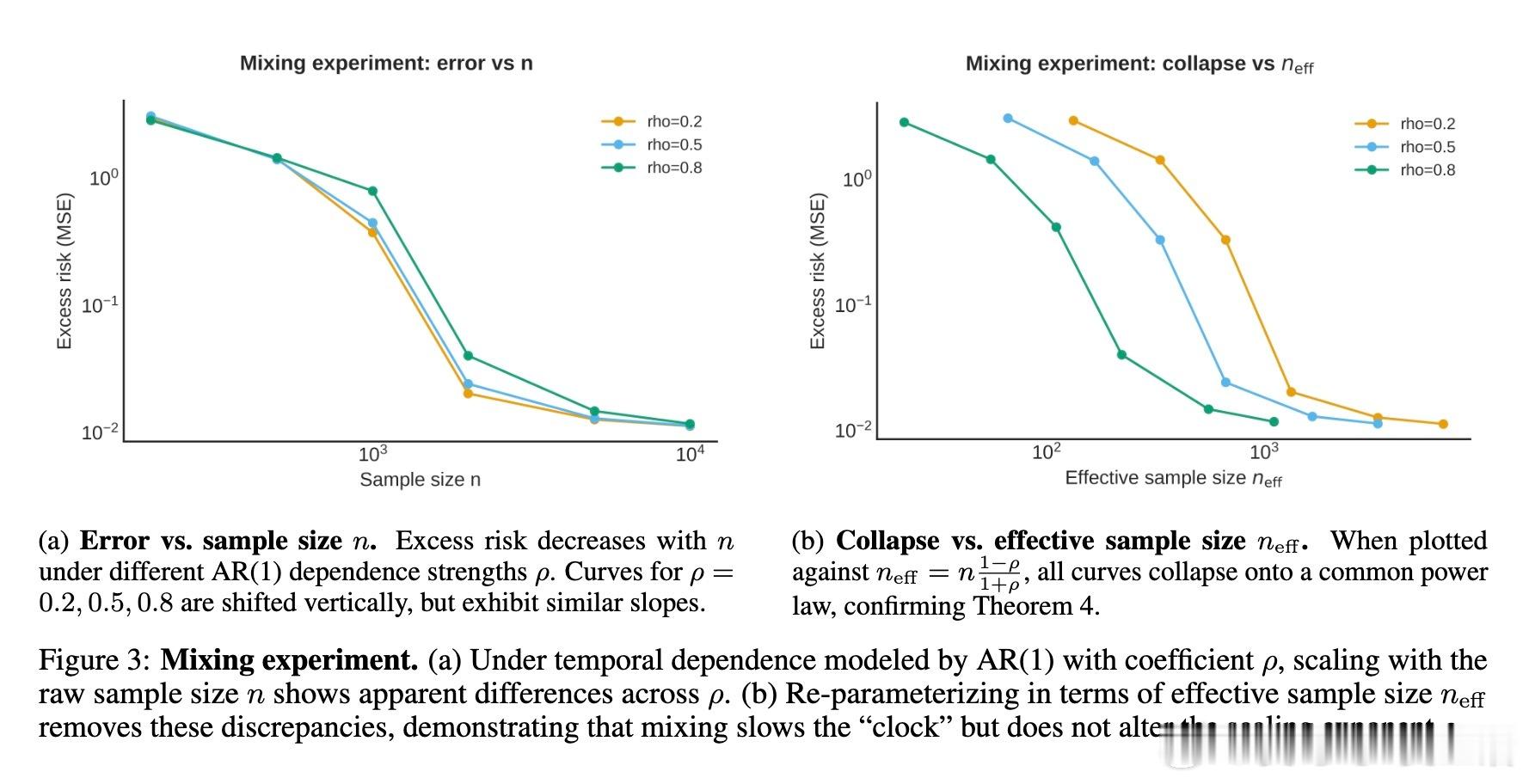
• 非独立同分布(非i.i.d.)数据通过有效样本数n_eff调整时间尺度,但不改变指数α,长期依赖减缓“时钟”而非曲线斜率。
• Transformer的尾指数β_tr由注意力头和MLP核的最重尾部决定,SGD早停等价岭回归,训练中如能通过特征学习减少冗余(提高β)则加速收敛。
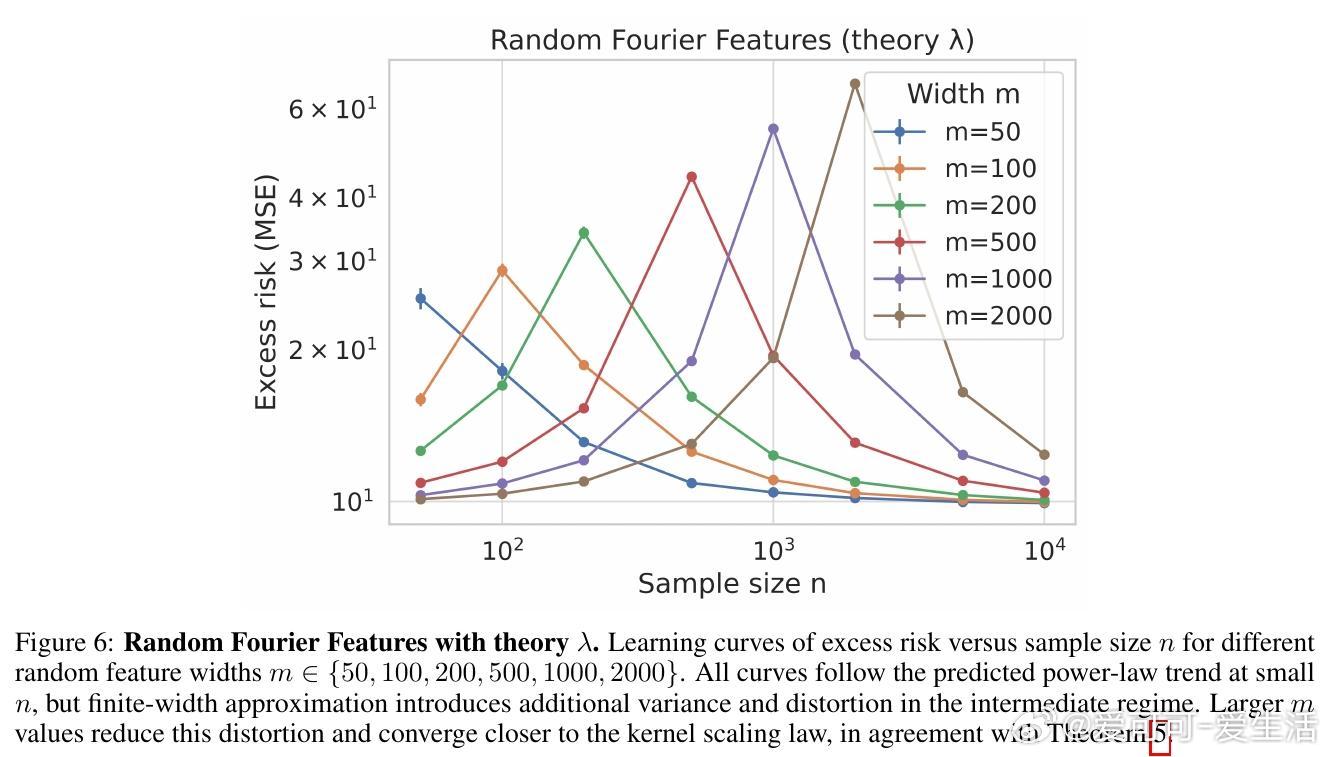
• 有限宽度随机特征需宽度m随样本量n多项式增长以保证指数不变,避免中间阶段的近似噪声。
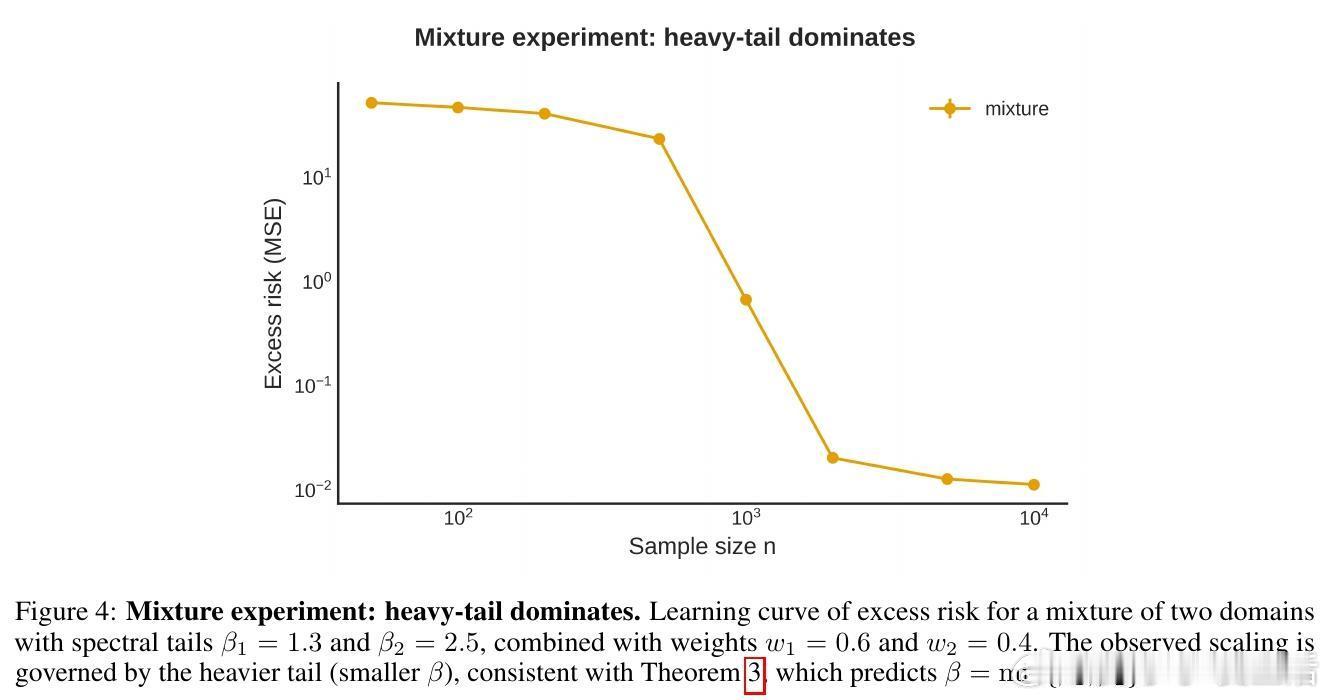
• 多域混合中最慢衰减的谱(最重尾部)主导整体学习曲线,意味着混合数据中瓶颈源于最高冗余成分。
• 理论为深度学习Scaling Laws提供统一数学基础,指导通过降低冗余提高扩展效率,如数据去重、光谱净化和架构优化。
心得:
1. Scaling Laws并非神秘普适规律,而是数据本身冗余结构的直接反映,表明提升性能的核心在于优化数据表示的有效维数。
2. 冗余指数β对模型设计和数据预处理具有直接指导意义,提升β即减少冗余,是加速学习的关键。
3. 理论框架的普适性涵盖了复杂依赖、混合分布及现代Transformer架构,提供了跨领域的可操作策略,突破了以往零散经验的局限。
详细了解👉 arxiv.org/abs/2509.20721
深度学习ScalingLaws机器学习理论Transformer核方法模型扩展