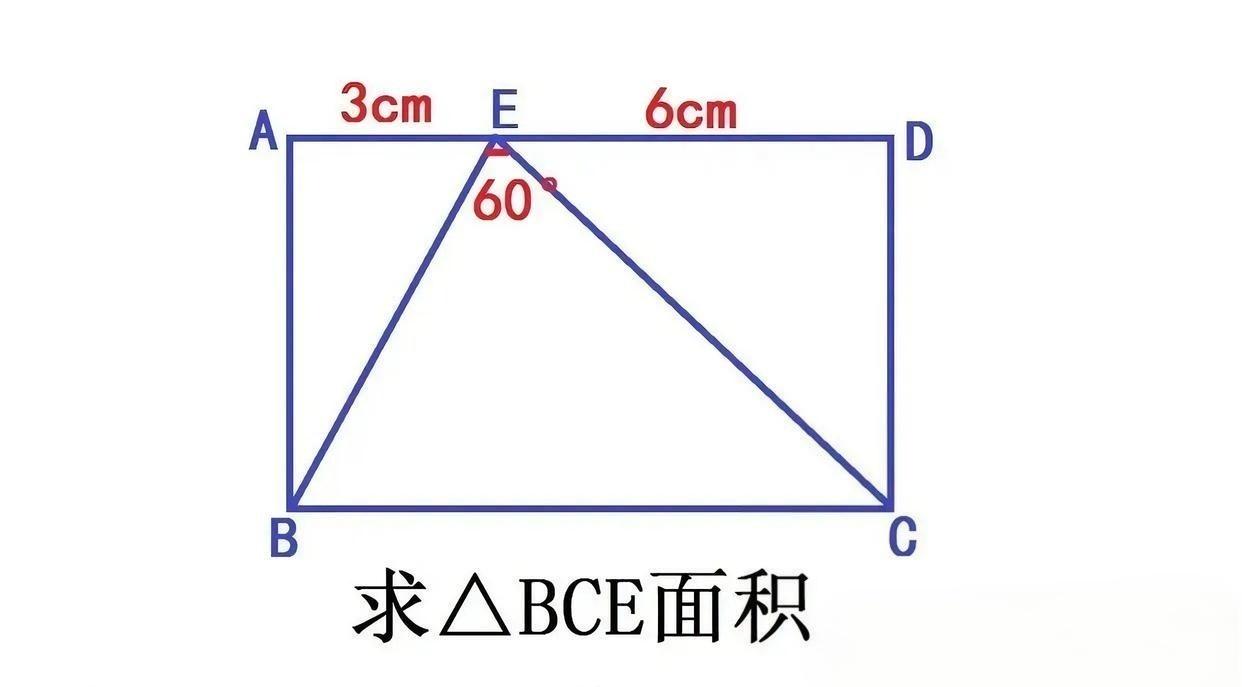
985家长被初中数学竞赛题难住?这道长方形里求三角形面积的题,藏着的可不是普通的解题思路! 乍看之下,已知边的长度和一个60度角,好像条件零散得摸不着头脑,常规的面积公式根本用不上。其实这道题的关键,是跳出“直接计算”的思维定式,把分散的条件通过几何变换串联起来。 与其死磕三角形本身,不如把目光放回长方形的特性上,给这个60度角找一个“几何载体”——构造特殊三角形是破题的核心。当你把线段和角度的关系,转化成等边三角形的特征时,那些看似无关的边长,就成了求解的关键线索。 原来初中数学竞赛考的从不是计算技巧,而是能不能跳出固有框架,用转化的思维把复杂问题简单化。不得不说,现在的初中数学题,真的把几何思维的灵活性玩到了极致!

![突然发现孩子还是有点情商的[呲牙笑]上周四数学周考孩子考了116,班级第一名,这](http://image.uczzd.cn/7654624206383666979.jpg?id=0)





JYYX
这题这题思路还比较直击 ,可以转化为解一元二次。但是不知道是不是我没算对,计算很复杂啊。 设AB长为x △BCE面积刚好是矩形的一半。也就是BE✘EC✘sin60=(3+6)✘X 再可以用勾股定理求得 BE EC的长度表达式。代入等式 就等到关于 X^2的一元二次方程。 不是为啥我算出来X^2的解带根号。
JYYX
这题思路还比较直击 ,可以转化为解一元二次。但是不知道是不是我没算对,计算结果带根号。 设AB长为X,利用△BCE面积刚好是矩形的一半得到等式。也就是BE✘EC✘sin60=(3+6)✘X。 再用勾股定理求得 BE EC的长度的X表达式。代入等式, 就等到关于 X^2的一元二次方程。 不是为啥我算出来X^2的解带根号。
张冠李戴
连接ac,S△adc=S△bce 沟股定理求出cd