[LG]《Best-of-∞ -- Asymptotic Performance of Test-Time Compute》J Komiyama, D Oba, M Oyamada [New York University & Institute of Science Tokyo & NEC Corporation] (2025)
最佳策略揭秘:如何用有限算力逼近无限采样的极限表现?
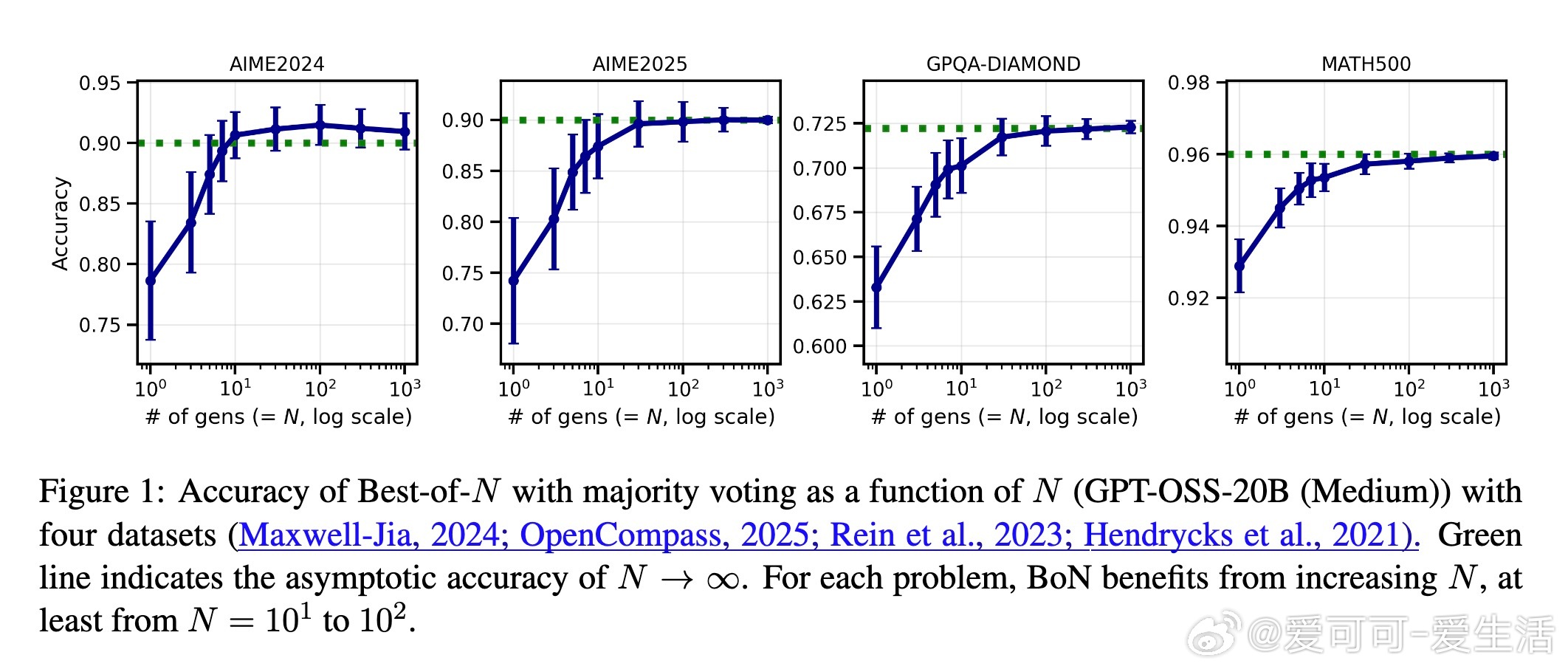
• 研究聚焦于大语言模型(LLM)在测试时通过“best-of-N”多数投票策略的性能极限,即N趋近于无穷大的best-of-∞表现。
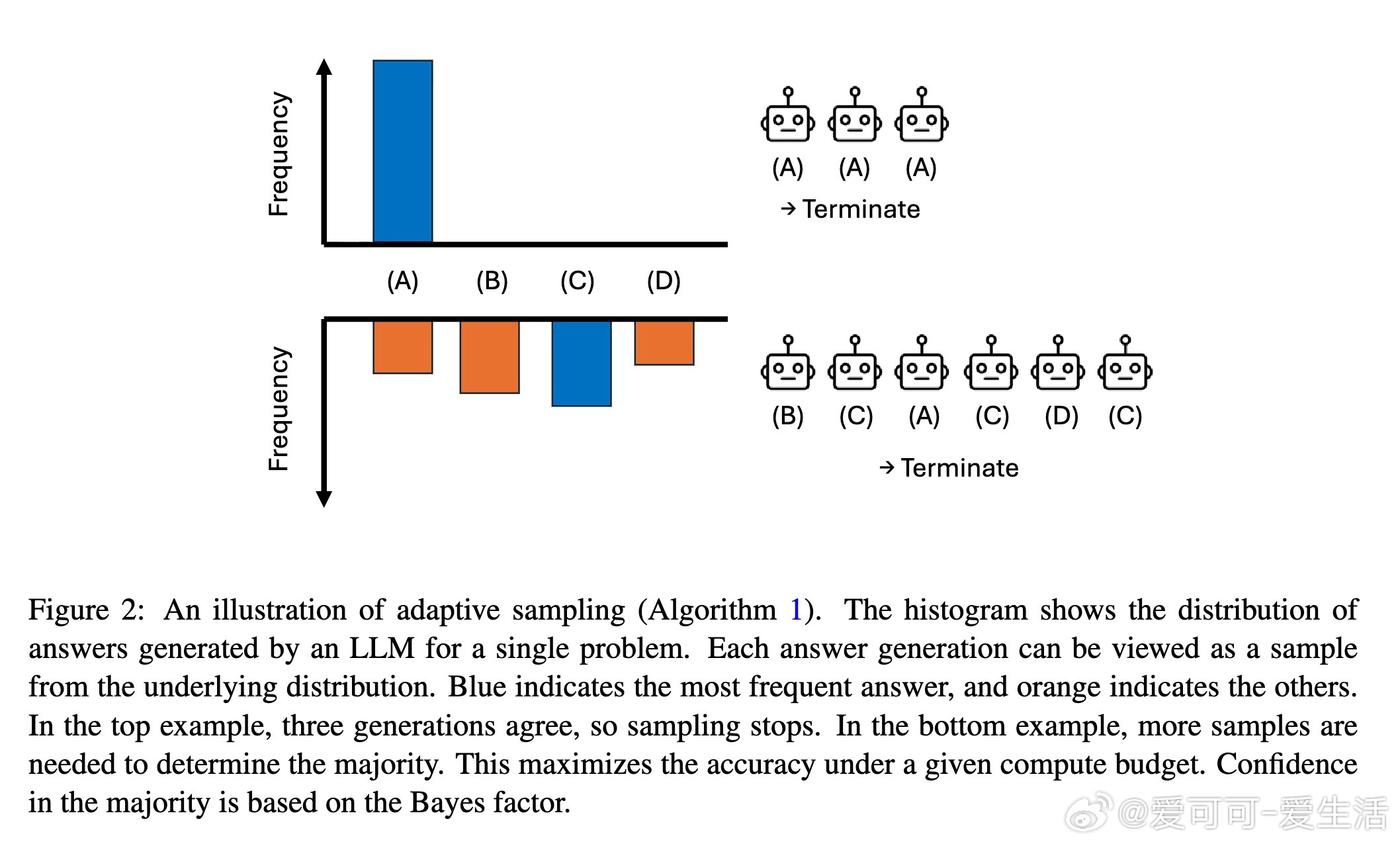
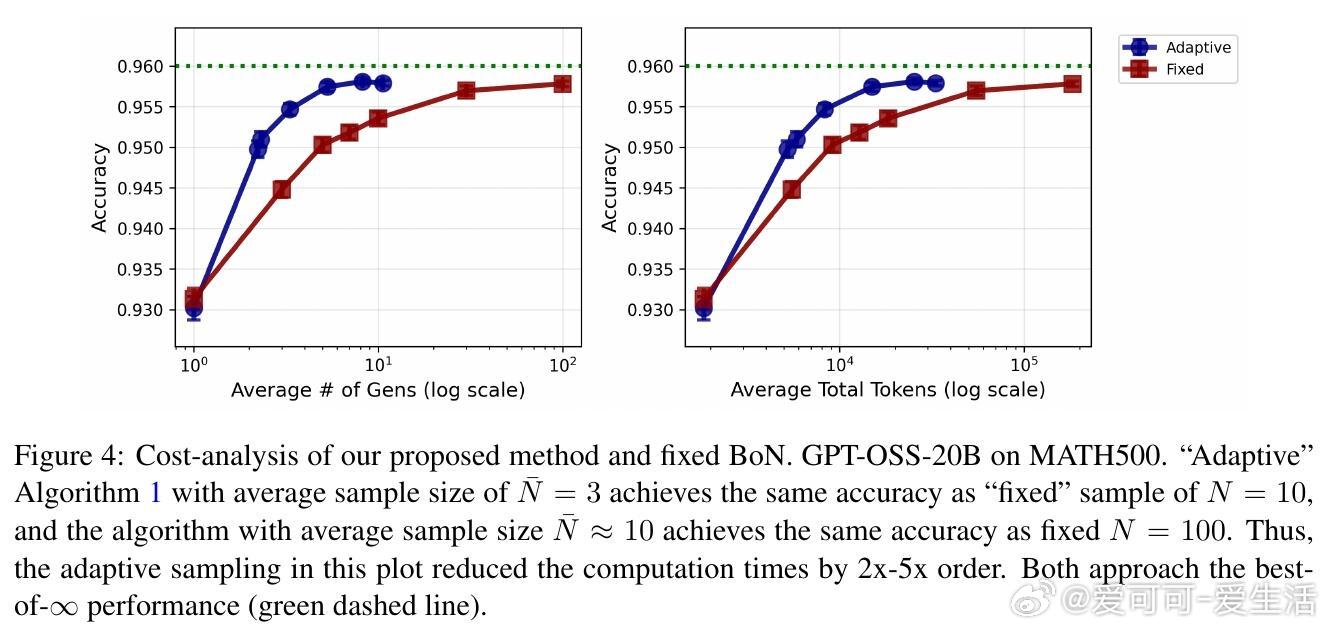
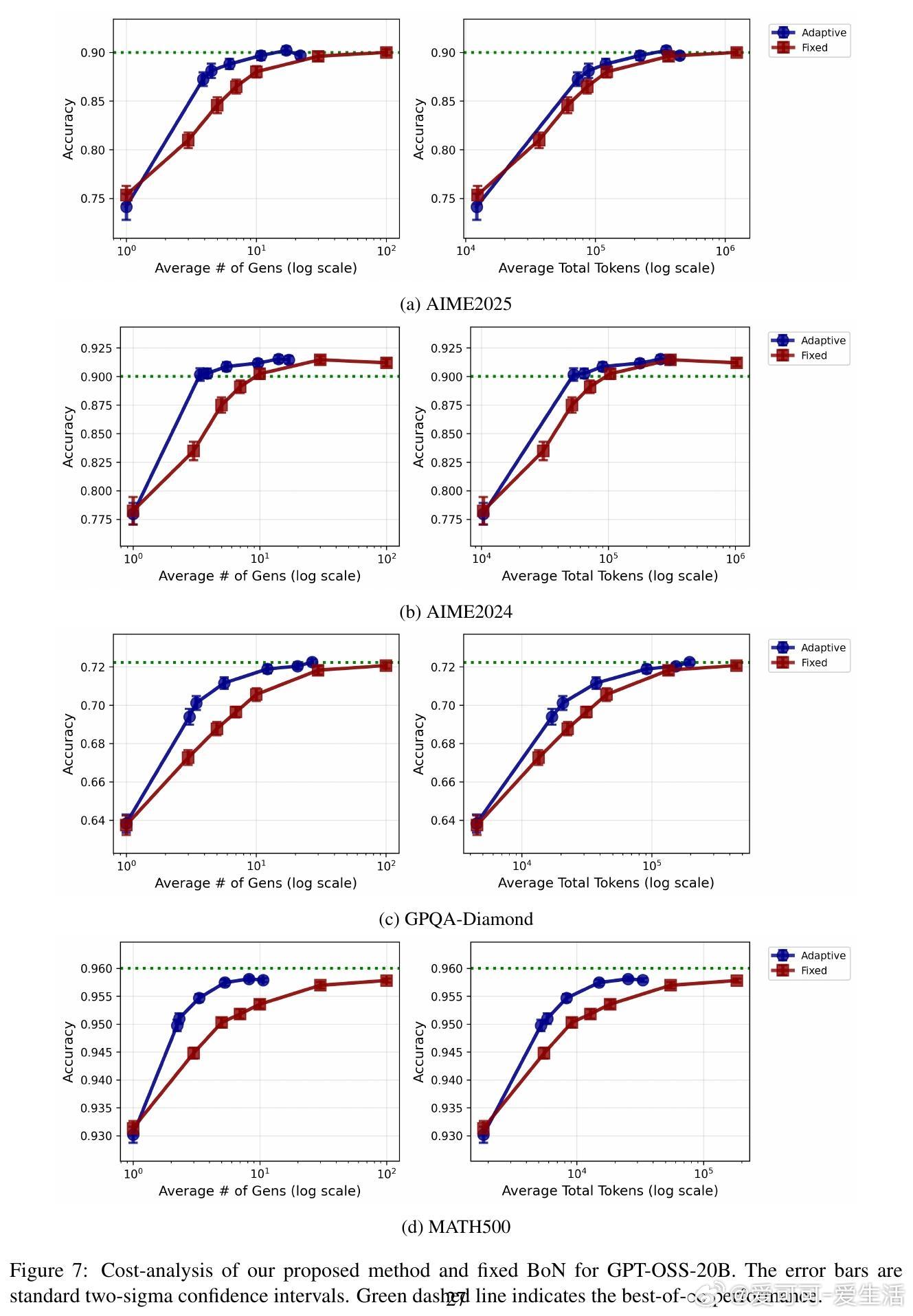
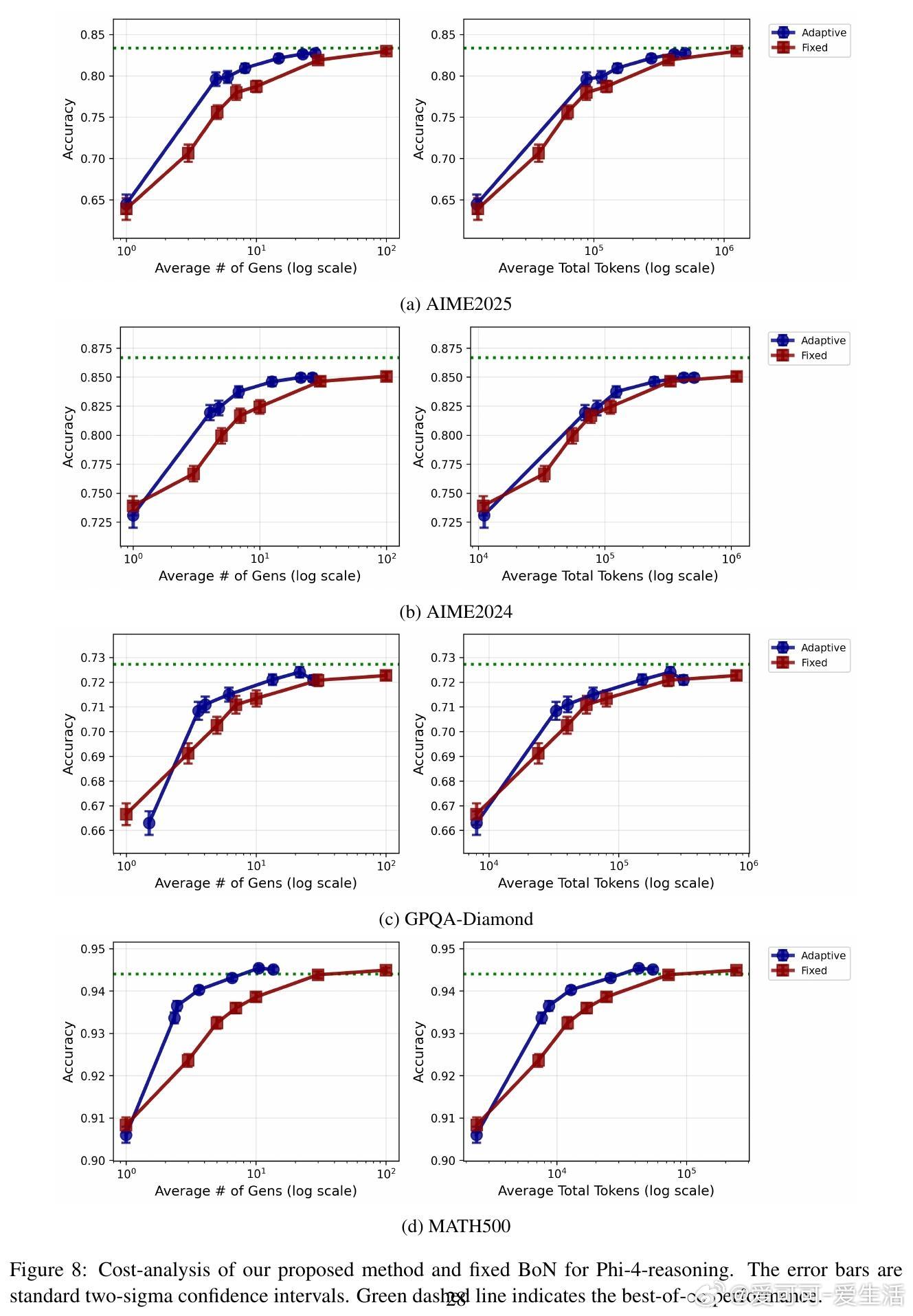
• 直接实现best-of-∞需要无限算力,论文创新性地设计了基于贝叶斯因子的自适应采样算法,动态决定生成答案数量,显著节省推理成本。
• 该算法利用Dirichlet过程先验,优雅应对答案空间可能无限的复杂性,实现统计置信度驱动的采样终止。
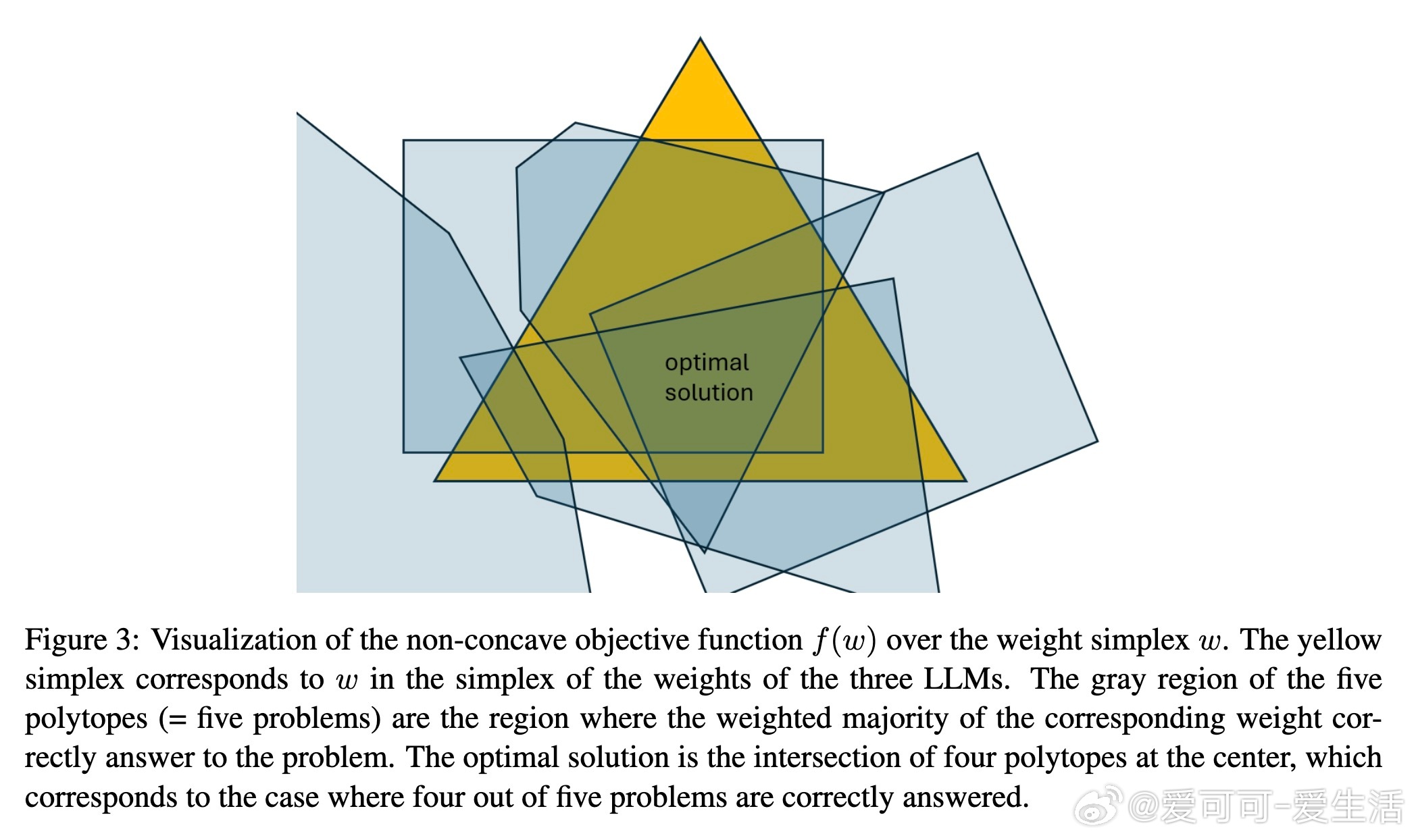
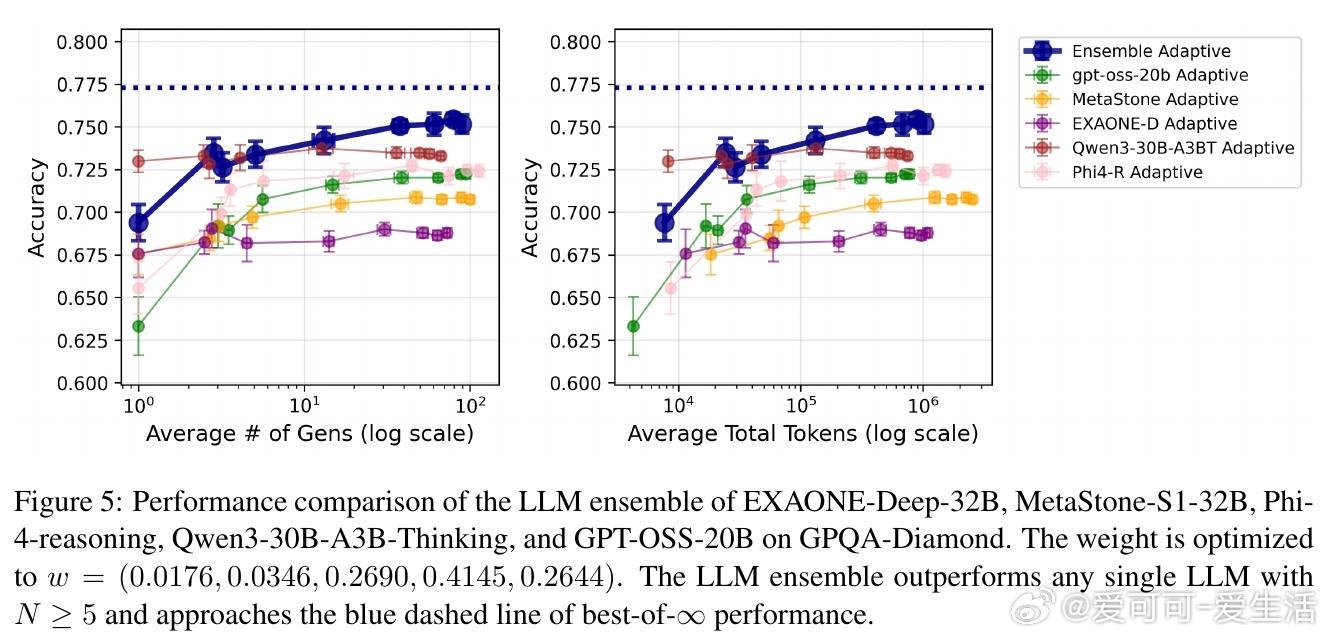
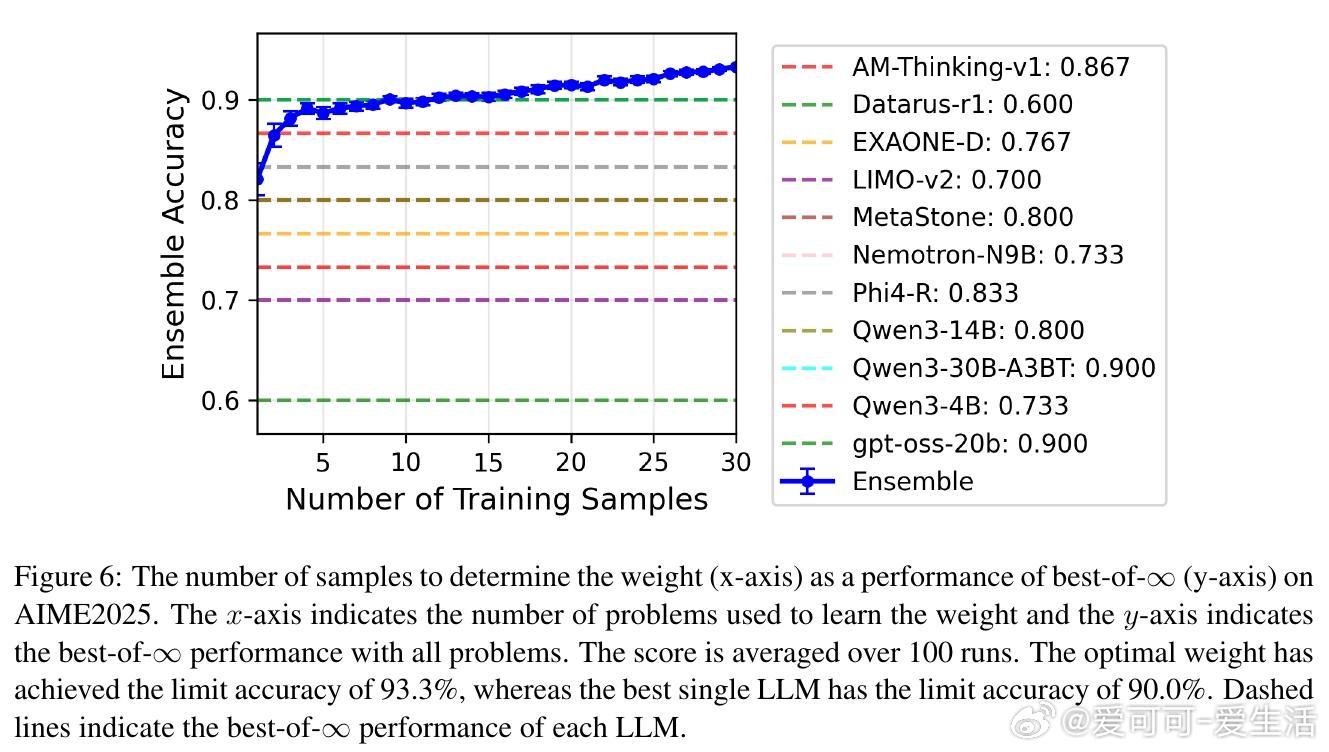
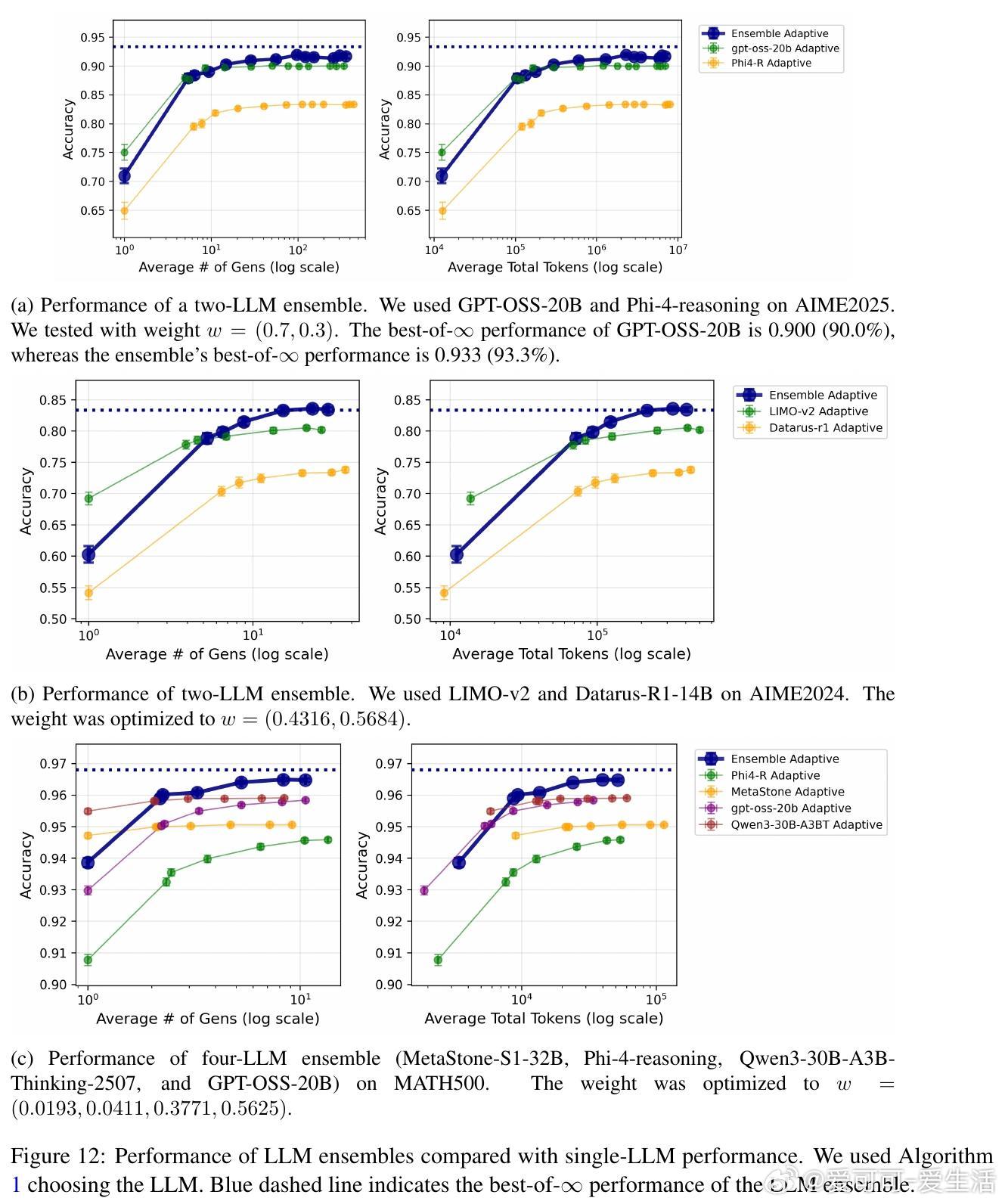
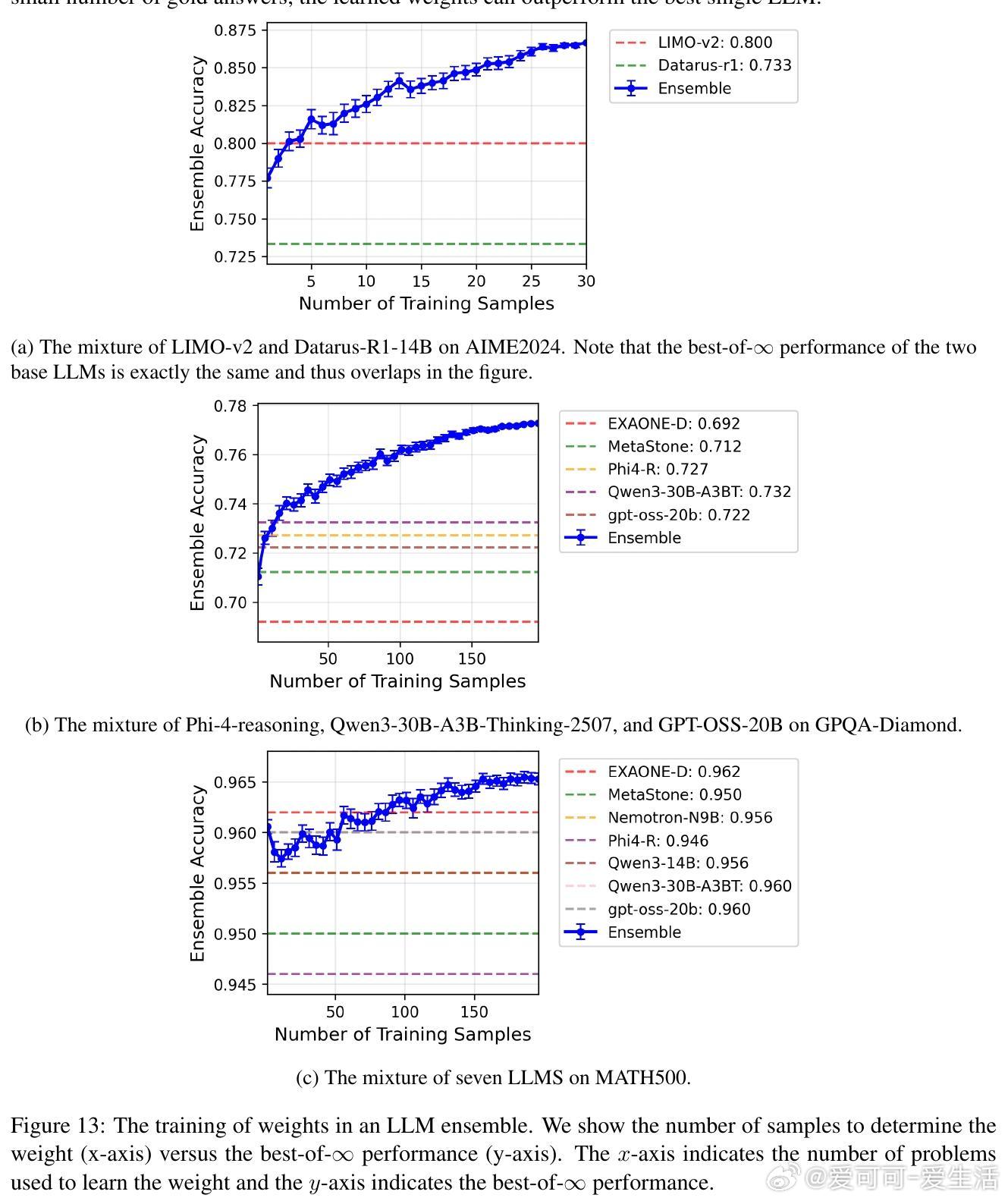
• 进一步提出了多LLM加权集成方案,通过混合整数线性规划(MILP)优化模型权重,超越单一模型表现,且权重优化具备理论收敛保证。
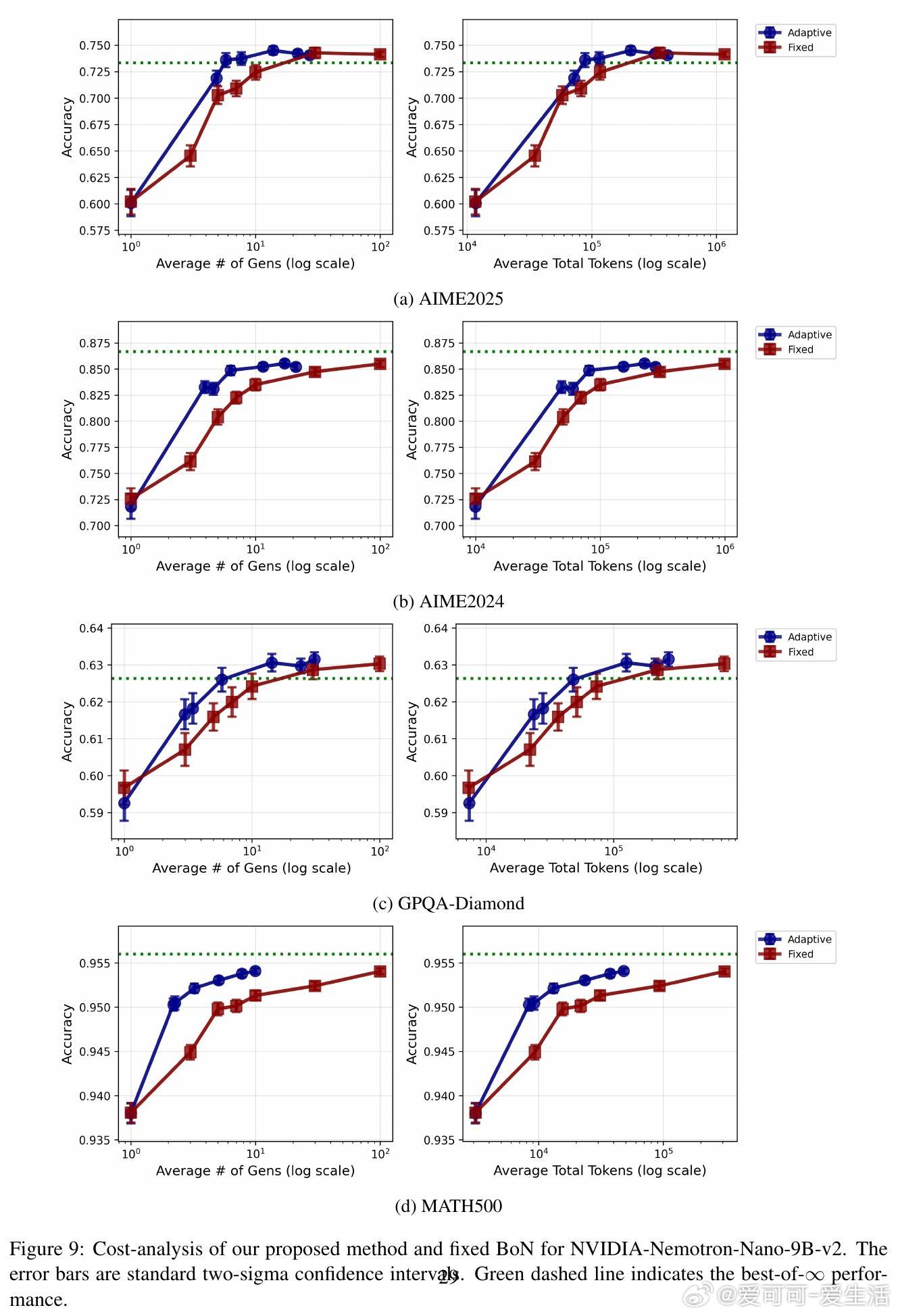
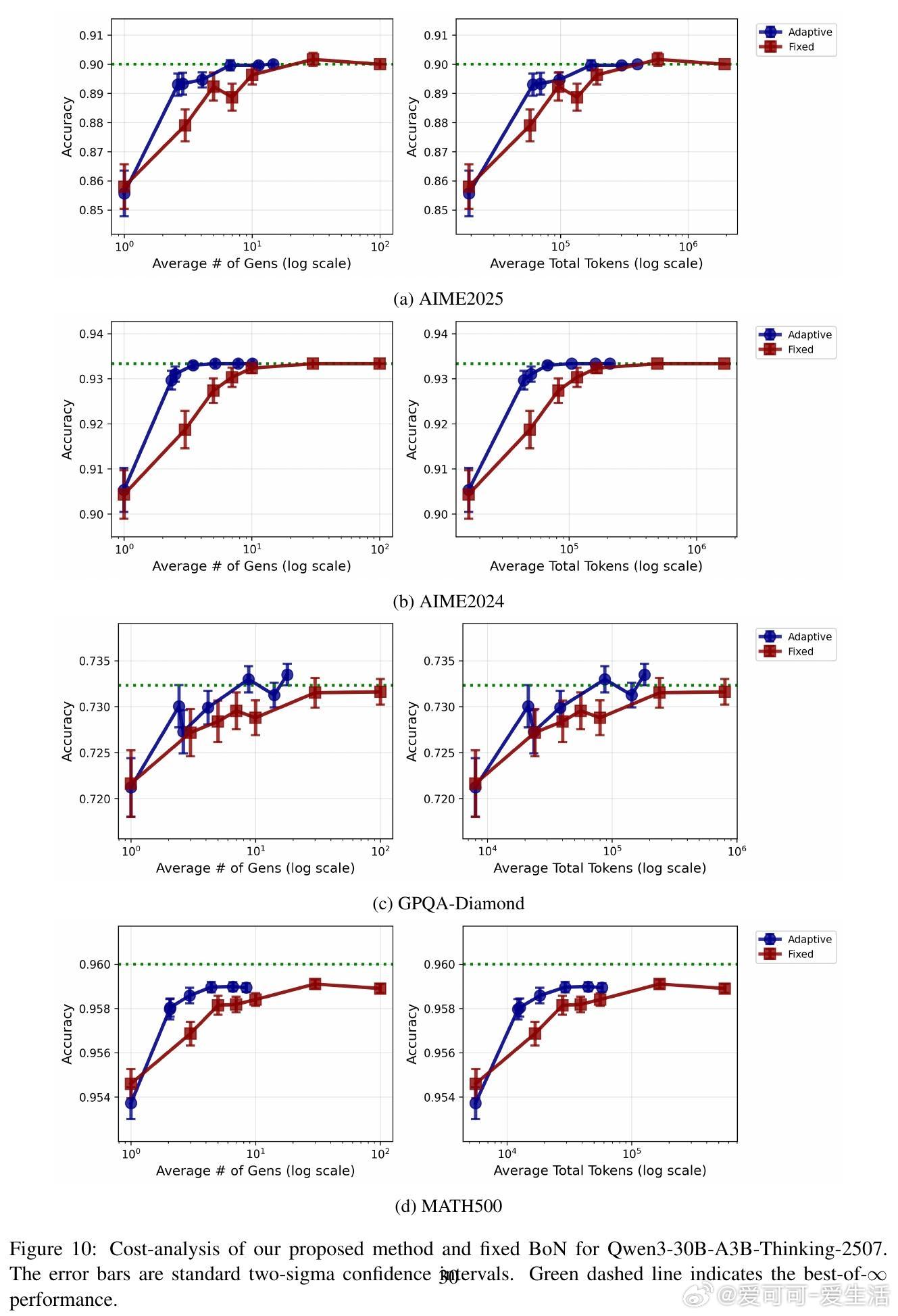
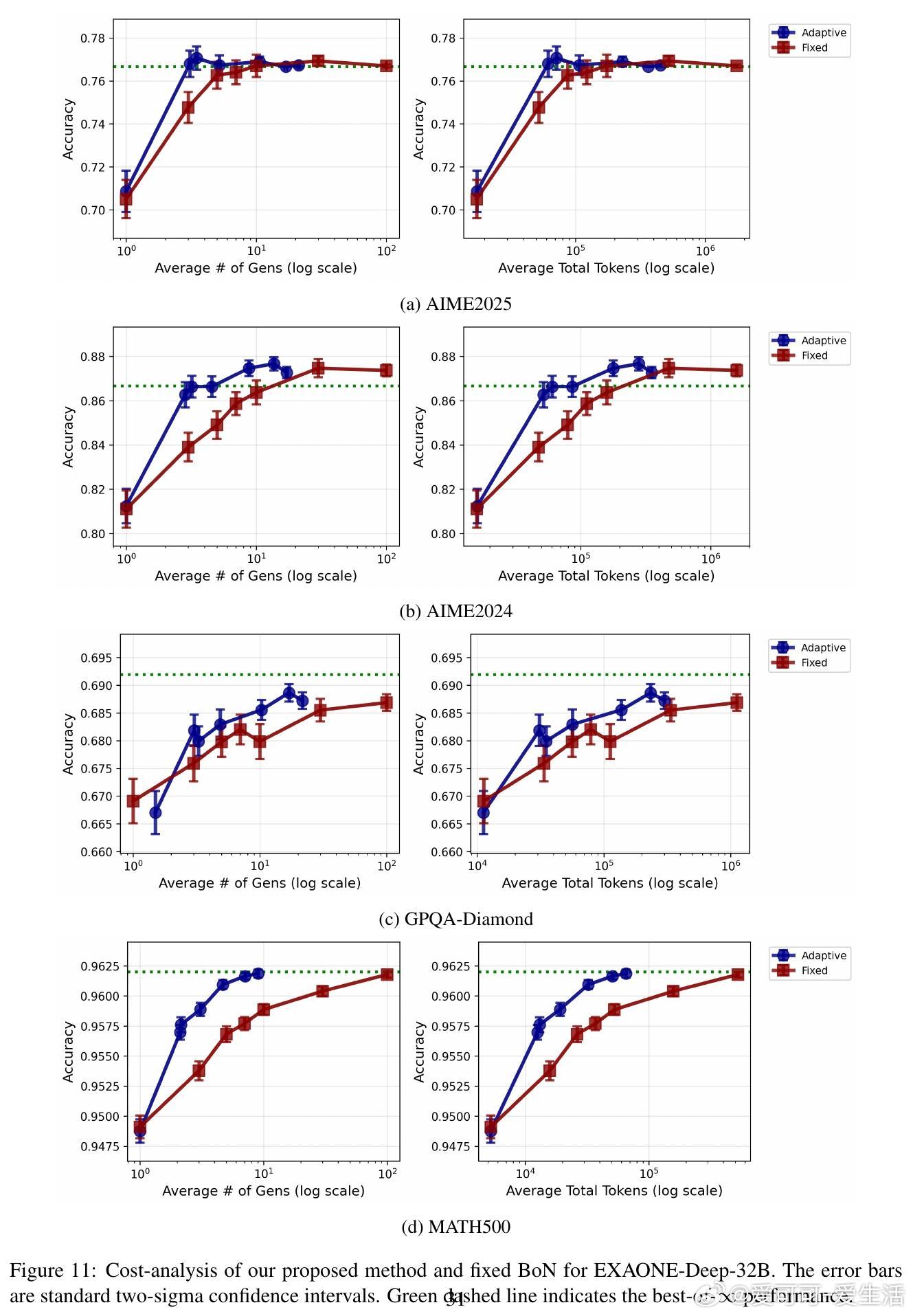
• 实验涵盖11款主流开源模型与4大复杂推理数据集(AIME2024/2025、GPQA-DIAMOND、MATH500),每对问题平均生成80+答案,远超以往研究规模。
• 实验结果显示:自适应采样比固定采样节省2-5倍计算资源;LLM集成稳健提升准确率;学习的权重具备良好泛化能力,且转移学习效果显著。
• 多种答案选择方法对比中,多数投票方法在最佳五选一场景下击败了基于奖励模型和LLM作为裁判的复杂策略。
心得:
1. 在有限算力条件下,动态决策何时停止采样远比盲目增加样本数更高效且准确。
2. 集成多模型的非最优成员可补偿单模型盲点,优化权重能挖掘这种互补性,极大提升整体性能。
3. 采用统计推断方法(如贝叶斯因子和Dirichlet过程)处理答案分布的未知性,为复杂生成任务提供了理论和实践上的双重保障。
详情参阅🔗arxiv.org/abs/2509.21091
大语言模型集成学习自适应采样贝叶斯推断推理优化